Les courbes elliptiques en cybersécurité et pentesting
Lire l'article
Introduction
Les courbes elliptiques sont devenues incontournables en cryptographie moderne, offrant un compromis idéal entre sécurité et performance. Leur capacité à fournir un haut niveau de sécurité avec des clés de petite taille en fait un outil privilégié en cybersécurité et lors d'analyses de pentesting.
Fondamentaux mathématiques
Une courbe elliptique sur le corps des réels est généralement définie par l'équation de Weierstrass :
$$ y^2 = x^3 + ax + b $$
Pour éviter les singularités, le discriminant doit être non nul :
$$ \Delta = 4a^3 + 27b^2 \neq 0 $$
L'ensemble des points sur la courbe, avec un point à l'infini, forme un groupe abélien dont la loi d'addition est essentielle en cryptographie.
Loi d'addition des points
Pour deux points distincts \(P = (x_1, y_1)\) et \(Q = (x_2, y_2)\) sur la courbe, la pente \(m\) se calcule par :
$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$
Les coordonnées du point \(R = P + Q = (x_3, y_3)\) résultent de :
$$ x_3 = m^2 - x_1 - x_2 $$
$$ y_3 = m(x_1 - x_3) - y_1 $$
Pour le doublement d'un point \(P\) (c'est-à-dire \(P = Q\)), la pente se calcule ainsi :
$$ m = \frac{3x_1^2 + a}{2y_1} $$
Représentation graphique
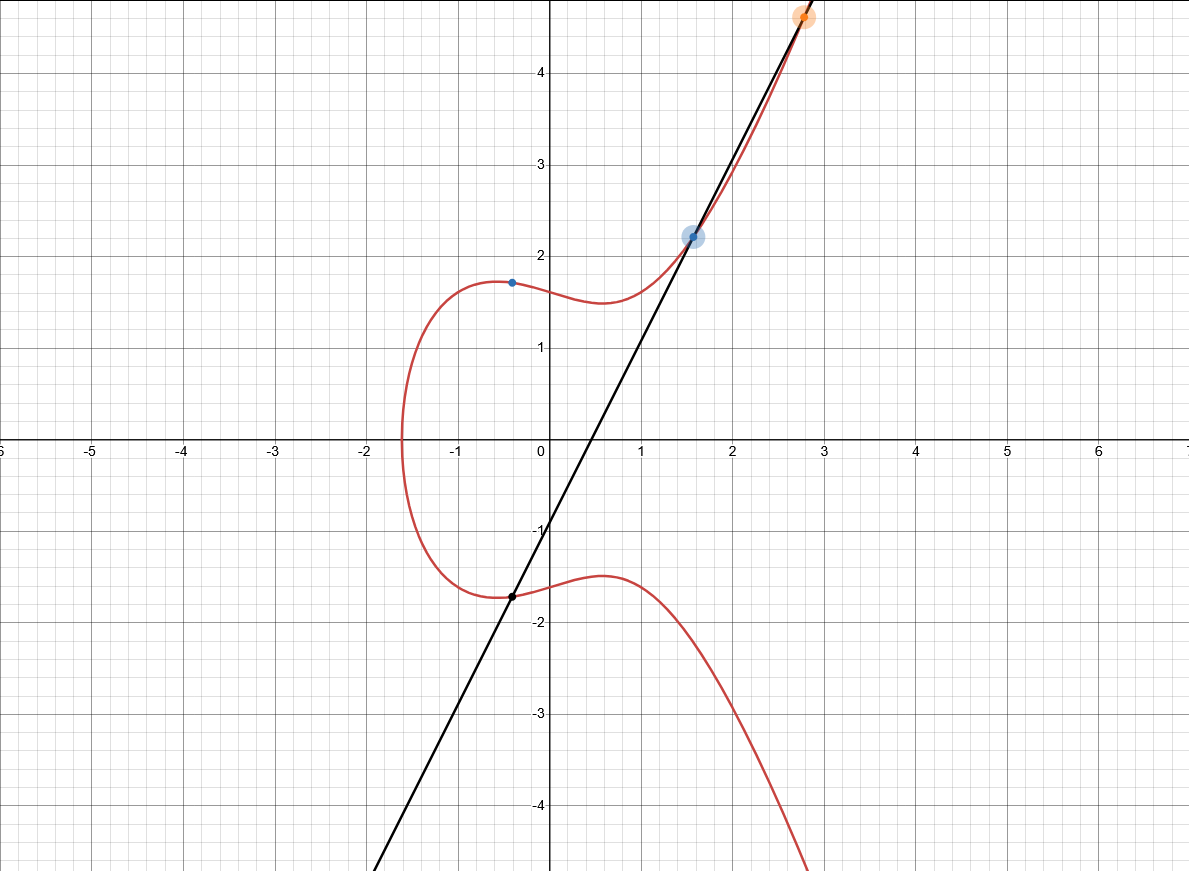
La représentation graphique d'une courbe elliptique aide à visualiser sa structure. Par exemple, la courbe :
$$ y^2 = x^3 + ax + b $$
peut être représentée graphiquement comme ci-dessous :
Utilisation en cybersécurité
La cryptographie à courbes elliptiques (ECC) offre plusieurs avantages :
- Clés de petite taille : Une clé ECC de 256 bits offre une sécurité équivalente à une clé RSA de 3072 bits.
- Efficacité : Les opérations ECC requièrent moins de ressources, idéal pour des environnements contraints.
- Sécurité robuste : Le problème du logarithme discret sur les courbes elliptiques (ECDLP) est difficile à résoudre.
Implications en pentesting
Pour les professionnels du pentesting, l'analyse des implémentations ECC est cruciale afin de détecter d'éventuelles vulnérabilités. Voici quelques points à vérifier :
- Validation des paramètres : S'assurer que \(a\) et \(b\) respectent les standards et que le discriminant est bien vérifié.
- Contrôle des points : Vérifier que les points reçus lors des échanges appartiennent bien à la courbe pour éviter des attaques par "invalid curve".
- Génération aléatoire : Une mauvaise implémentation peut compromettre la sécurité des clés privées.
Exemple de code d'audit en Python
def is_on_curve(x, y, a, b):
# Vérifie si y² = x³ + ax + b
return y**2 == x**3 + a*x + b
# Exemple pour la courbe: y² = x³ - x + 1
a = -1
b = 1
x, y = 2, 3
if is_on_curve(x, y, a, b):
print("Le point est sur la courbe")
else:
print("Le point n'est pas sur la courbe")
Approfondissements et recherches avancées
La robustesse de l'ECC repose sur la difficulté du problème du logarithme discret sur courbes elliptiques (ECDLP). Pour un point \(P\) et un entier \(k\), le calcul du point \(Q = kP\) est rapide, mais retrouver \(k\) à partir de \(P\) et \(Q\) reste un problème complexe :
Q = kP